UTF-8 Hash Compression
As I was reading about UTF-8 the other day, I read on wikipedia, that the size of a given character was anywhere from 1-4 bytes.
UTF-8 and Ascii use an unbelievable amount of storage per amount of text actually stored on disk
I knew that there had to be a better way. What if, instead of storing every word, we had every single word in a database with a hash associated, using a mere 2 bytes we could support 65,535 unique words; well within the scope of most data. Then, by merely transferring the dictionary beforehand, we could save data in high performance or high volume applications.
So what did I do? I wrote up some python scripts and did some quick statistical analysis to see if my method made any sense.
The first thing I did was head over to Project Gutenberg (A free online database of books) and download a few books in txt (UTF-8) format.
After obtaining several books, I decided to concatenate them into one larger file to make for easier reading in python. To do this, I used a little bash wizardry:
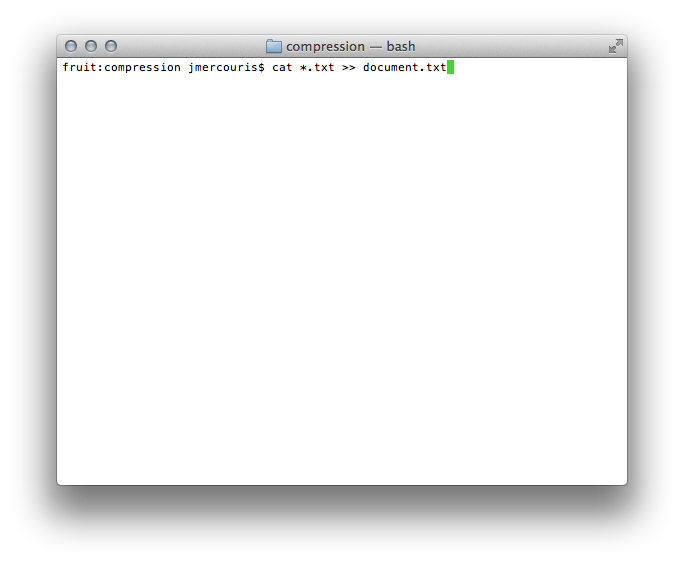
What this simple command does is uses cat to output to the terminal, then using redirection indicated by the >> I redirect the output to the file called document.txt.
Python Statistics: Code!
Afterwards I began working on my python programs. The first one I needed was to measure the length of my amalgamated file.
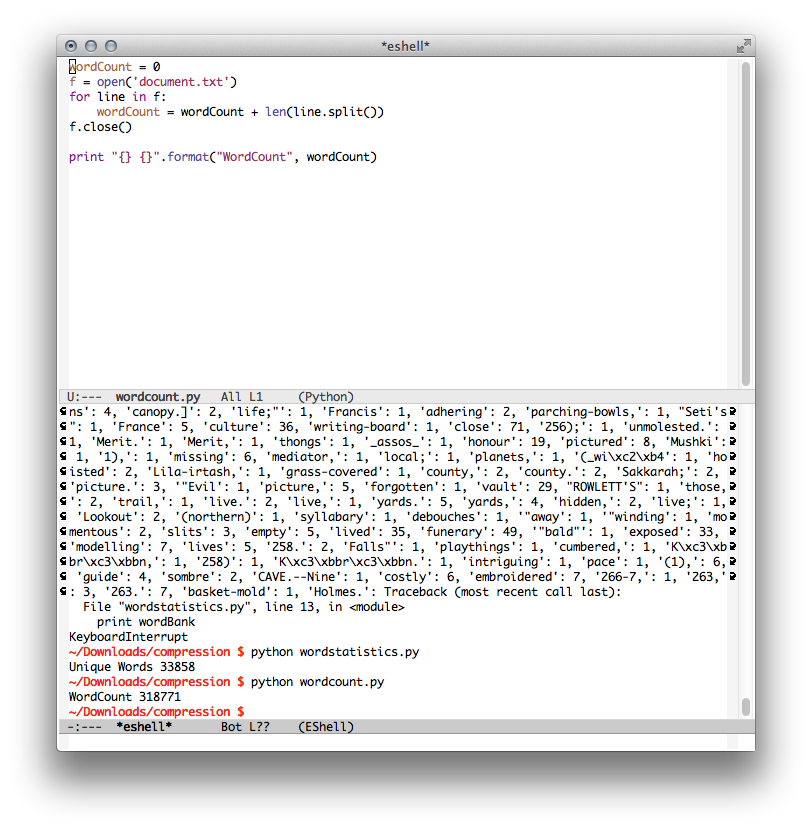
A relatively simple program, it just reads a file line by line, and iterates through increasing the count. At the end of all computation it spit out a number of 318,771 total words.
The second program that I made was a little bit different. I wanted to know who many unique words there were in the text. This one is a little bit more complex:
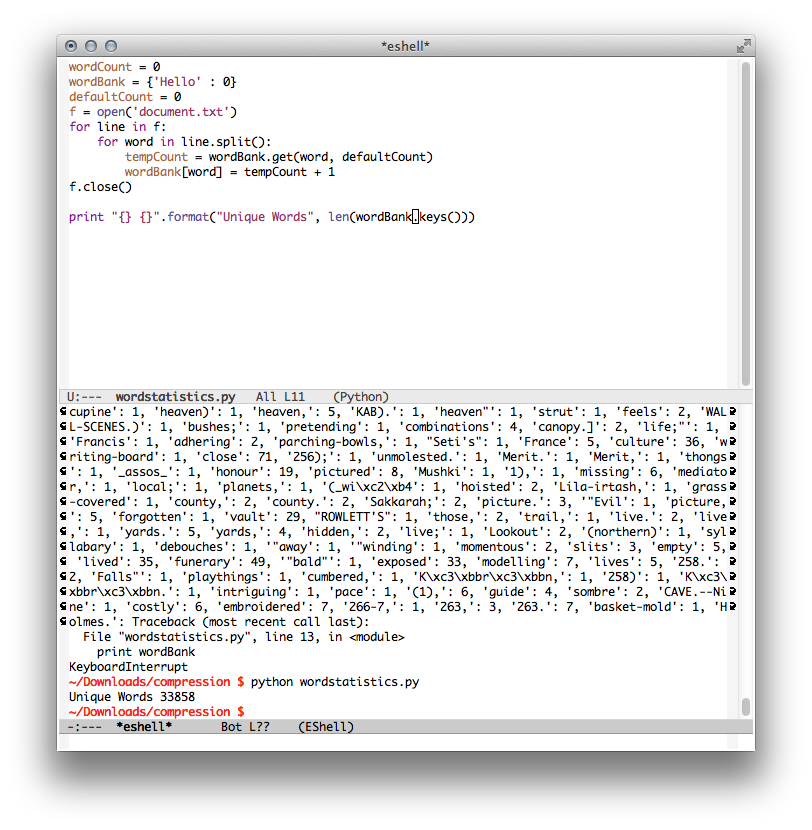
What this code does is creates a dictionary. Then, using the word as a key, it counts to see how many unique words there are within the texts. In this case there were only 33,858 unique words among the 318,771 words. That means, there were 9.41x too many symbols in plain uncompressed ascii being duplicated throughout.
Traditional Compression
I know that compression looks for patterns within binary and does something similar to my proposed method. Let's see how binary compares to the theoretical gains proposed in my method. First let's look at the original file:
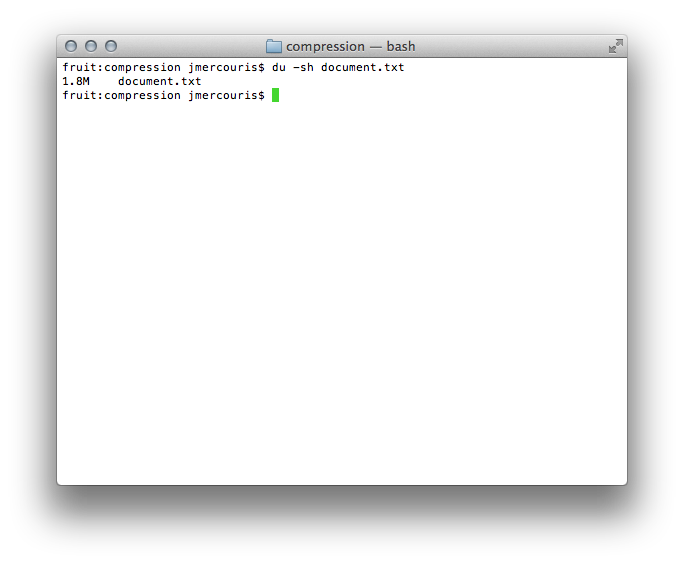
A full 1.8m! That's a rather large text file; let's see what compression can do for us:
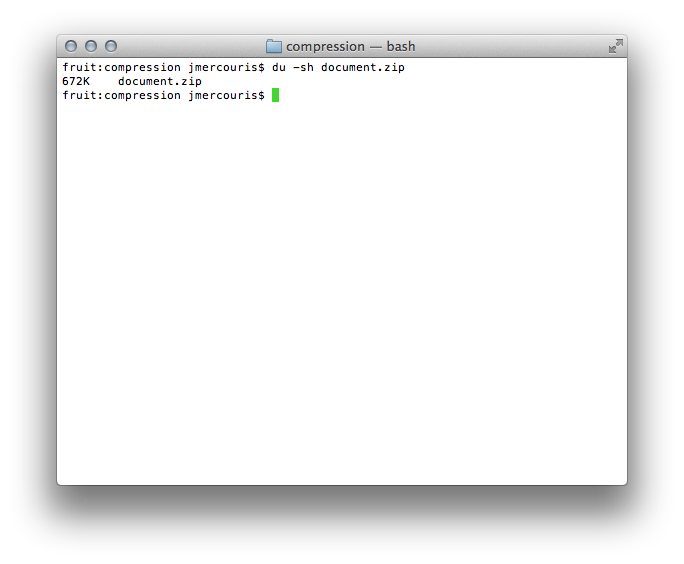
Still, 672K! That is a reduction of roughly 65%, but still not anywhere near the theoretical limits.
If we take my method, and agree to a predefined dictionary file that we distribute. The dictionary file might look something like the following:
00000001 = "hello"
00000010 = "oh"
...
11111111 = "goodbye"
we could theoretically transfer the same document using only 639.89 KB. Using different documents, I've seen a difference of anywhere between 5% to 15% gain over traditional compression methods. Though hardly practical, it is an interesting idea.
Conclusions
Typically, words in the english language are 5 letters long.
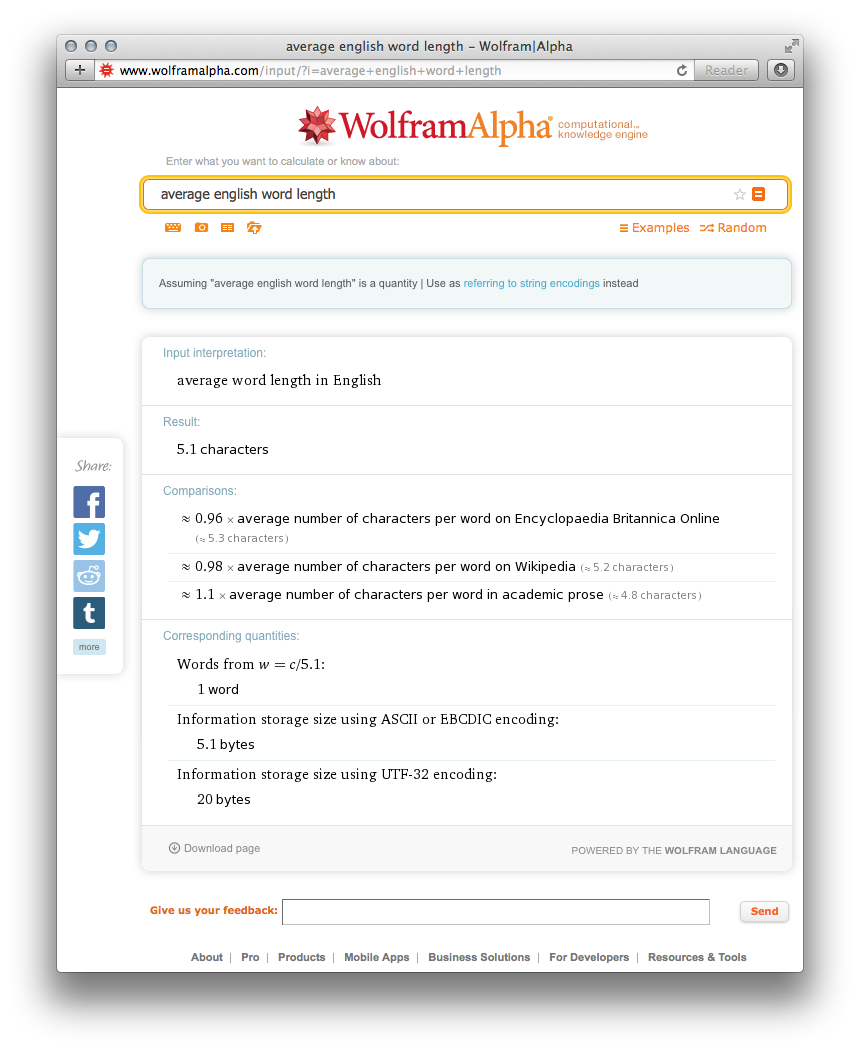
Each letter in the word, in UTF-8 occupies approximately ~1byte. Therefore, a given word is approximately 5 bytes, using this methodology it may be possible reduce the load to only 2 bytes per words for commonly used words; and; because everything is in a hash, we can do it in O(1) time.
Get the Code:
If you want to download the sample code and the project, please visit the bitbucket link below to download/clone it.